Program to Search in Row-wise and Column-wise Sorted Matrix

We will be writing a program to search in row and column sorted matrix. i.e. printing the location of an element, if it exists.
Given: (m x n) sorted Matrix, number to search.
Output: Location of the given number if found or “Not Present” if not.

Understanding how a sorted matrix gives us extra information

The conventional one-by-one traversal of a matrix to check for a given number would surely work, but its time complexity (number of operations required to reach the output) would be of the order m*n, as the program will traverses each number of the matrix.

The extra information of the matrix being sorted in both rows and columns gives us a peculiar advantage, to understand what this power is considered the following.

Example of row and column sorted matrix:

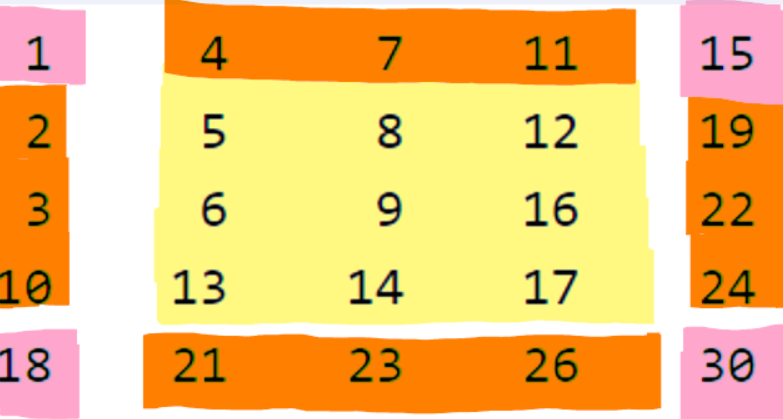
In a matrix with 5 rows and 5 columns, we’ll divide the matrix into 3 types of elements,

1. The Corner Elements(Pink)- The numbers in the four corners of the matrix.
2. The Border elements(Orange)- The numbers in the border except for the corner elements.
3. The Bulk elements(Yellow)- The numbers in the rest of the bulk of the matrix.

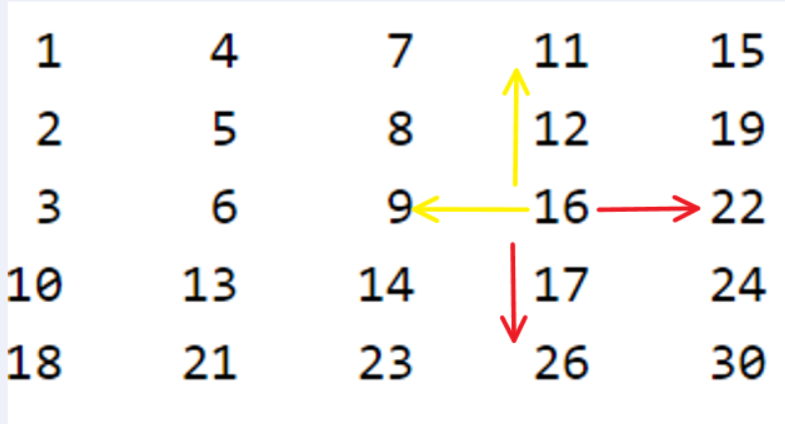
We pick any random location in the matrix from the bulk elements(i.e. index < 4), let’s say at [2,3] the number 16, for this and any other similar point we can say the following points with certainty,

Any number having,

• Row index > 2 is also greater than 16(red arrow) and vice versa
• Column index >3 is also greater than 16(red arrow) and vice versa

Next, let’s select a random location from the border elements, let’s say at [4,3] the number 24, for this and any other similar point we can say the following points with certainty,

Any number having,

• This is the largest element in the row with an index of 3.
• Row index > 2 is also greater than 24(red arrow) and vice versa
• Column index <3 is also less than 24(yellow arrow).

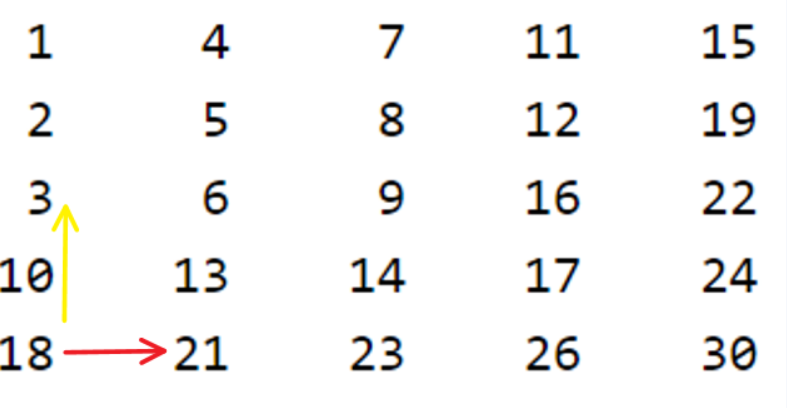
Lastly, let’s select a random location from the border elements, let’s say at [0,4] the number 18, for this and any other similar corner point we can say the following points with certainty,

Any number having,

• This is the smallest element in the row with an index of 4.
• This is the largest element in the column with an index of 0.
• Row index < 4 is also less than 18(red arrow)
• Column index >0 is also less than 18(yellow arrow).

So if we are at a particular corner we are at highest/lowest of the row/column depending on which corner we are at. This is the additional information we are going to utilize in order to increase the efficiency of our algorithm. To hint at the solution, we will start at one of the corner points and work our way towards the number closer to the given number.

Visualization of row-wise and column-wise sorted matrix

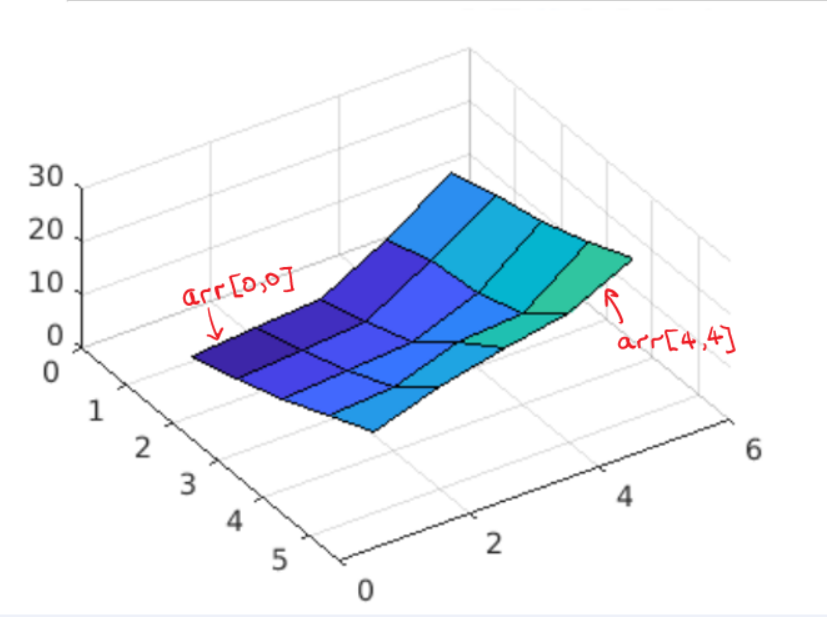
Another good way to visualize this is using this surface plot for the matrix values, whatever be the values of the matrix the shape and the grading of the surface will remain the same, the smaller numbers in purple shades, and the lighter blue shades representing the higher numbers.

Program to Search in Row-wise and Column-wise Sorted Matrix

Below is the efficient implementation of Search in Row-wise and Column-wise Sorted Matrix in C plus plus. Same logic can be implemented in other programming languages as well.

void search(int mat[4][4],int R, int C,int n)  //Function inputs: Matrix,Rows,Columns and given number
{
    int i = 0, j = C-1;    //initializing variables to start at top right corner.
    while(i < R && j > -1)   
    {
        if(n == mat[i][j])
        {
            cout<<"("i", "j")"; //if the number is found print its location and stop the execution
            return;
        }

        else if(n < mat[i][j])  //else if, the number is less move to the left column, by decrementing j
            j--;

        else if(n > mat[i][j])   //else if, the number is larger move downwards and hence increment i
            i++;
    }
    // if the while loop is executed fully, then the number must not present in matrix.
    cout << "Entered number not present"; 
}
    
int main() {  
    int arr[4][4] = {{10,20,30,40},  //Initialization
                     {15,25,35,40},
                     {27,29,37,48},
                     {32,33,39,50}};

    search(arr, 4, 4, 39);   //Main function, calling the above search in matrix function.

    return 0;
}

Approach to the algorithm:

As hinted above we will start with our traversal variable at the top-right corner of the matrix and compare this location’s number to be searched. One of 3 choices will result:

1. The number is equal to the given number:
   We output the current location and stop the further execution of the program, as the objective has been achieved.
2. The number is greater than the given number:
   This means that we have to go towards a location lower than the current one, as we are starting at the corner, this means we only have a single choice i.e. towards the left, so we decrease the column index (j) by one, and run the loop again.
   By doing this we can with certainty mark out the entire column as the numbers only increase downwards.
3. The number is less than the given number:
   Similar to the above discussion, we only have a single choice i.e. go lower and hence we increase our row index (i) by one.
   Again, we can mark out the entire row as the numbers only increase decrease towards the left.

The condition for the while loop is simply keeping the row and column indices in bounds. As we are decreasing column indices they should be positive, and increasing row indices should be less than the number of rows. And the loop will execute till it has found the location of the number crossed the boundary of the matrix.

Time Complexity of this algorithm

In the worst case, we will have to traverse the whole row first and then the column for a total of m+n iterations, which gives us a time complexity of O(m+n)

If we talk auxiliary space then it will be O(1). As we haven’t used any extra asymptotic space while implementation.

Exercise: Alternative solution

You can start the same code while starting at the opposite corner of the matrix, What do you think would be the modifications in the code for the same? Try it for yourself and discuss it in the comments section below.