Program for Spiral Traversal of a Matrix

We’ll learn to write a program for spiral traversal of a matrix of size m x n, which does mean as it sounds, we’ll start the corner of the matrix and traverse in a spiral towards the center of the matrix.

Understanding the question, and output

Given: Matrix, Size
Output: Printing elements in a line using spiral traversal of a matrix

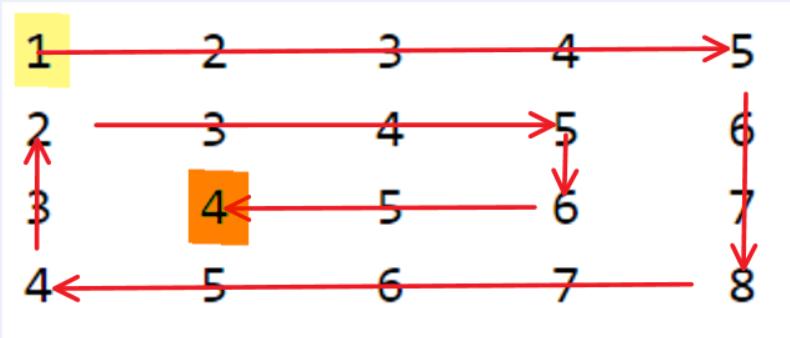
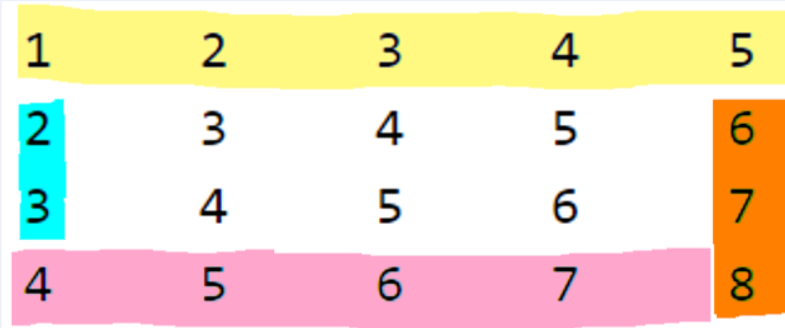
In the first image, we can easily visualize the objective, we want to start at the yellow top left corner and print the boundary elements and then start all over again till we have traversed all the elements of the matrix. The right image hints towards the solution approach for the program, can you guess

Approach to the algorithm

Here we’ll try to first find the basis and approaches towards the solution and with each next step the solution will become a bit more concrete,

Peeling an onion analogy:

To solve this problem, imagine we are peeling an onion, only here the onion is a matrix of R x C elements,

1. Consider we are printing our matrix’s boundary elements.
2. Then we peel off one row and column from each side. Basically, the elements we just printed.
3. We are left with a smaller matrix with R-2 x C-2 elements.
4. We again print the boundary elements and discard the elements we just printed.
   We repeat this process till we traverse all the elements

Breaking down the code into steps:

Let’s break it down into its components. Within one iteration we have to traverse the boundary elements once in a clockwise order

• Now in each iteration essentially we have to print the following 4 vectors to print.
  1. The top row is printed from left to right.
  2. The right Column is printed from top to bottom.
  3. The bottom row is to be printed from right to left.
  4. The left column is to be printed from bottom to top.
• Now we redefine the 4 boundary variables top, right, bottom, and left.
• We repeat these 3 steps top-down till we are out of elements, to check for it we’ll understand the stopping conditions for the outer loop next.

Now lets look at the program and it will click into place much faster, try to guess what must be the reasoning for the

Program for spiral traversal of a matrix

void printSpiral(int mat[4][4], int R, int C) //Function declaration
{
    int top =0,left =0,bottom= R-1,right=C-1;   //initializing variables for the boundaries
    while(top<=bottom && left<=right) // Condition:Crossing of top and bottom or left and right should not take place
    {
        for(int i=left;i<=right;i++)  //Top row traversal left to right
            cout<<mat[top][i]<<" ";
        top++;                        
        for(int i=top;i<=bottom;i++)  //Right column traversal top to bottom
            cout<<mat[i][right]<<" ";
        right--;
        for(int i=right;i>=left;i--) //Bottom row traversal right to left
            cout<<mat[bottom][i]<<" ";
        bottom--;
        for(int i=bottom;i>=top;i--) //Left column traversal bottom to top
            cout<<mat[i][left]<<" ";
        left++;
    }
}
int main() {
    int mat[4][4],val=10;
    for(int i=0; i<4;i++)
    {
        for(int j=0;j<4;j++)
        {
            mat[i][j]=val;  //Initialization of matrix
            val++;
            cout<<mat[i][j]<<" ";
        }
        cout<<endl;
    }
    cout<<endl;
    printSpiral(mat,4,4);  //Function Call
}

Output:
10 11 12 13 
14 15 16 17 
18 19 20 21 
22 23 24 25 

10 11 12 13 17 21 25 24 23 22 18 14 15 16 20 19

End Condition for the outer loop

For simplicity, first, consider the top and bottom variables. We are increasing the top variable by one after each iteration, similarly, the bottom is being decremented. There will come a point when top will be less than bottom, and we can ensure that all the elements have been traversed.
We can similarly see the same pattern for the left and right variables, and both of the conditions should be simultaneously satisfied or else we are repeating elements. This explains the choice of the ‘&&’ operator

Time complexity of spiral traversal of a matrix

As we are traversing each and every element of the matrix the time complexity will be O(R*C). Can you think of a solution more efficient than this? Hint: Think about it, is it even possible?

Related: Write a program to search in row and column sorted matrix efficiently