Maximum Sum Circular Subarray | Leetcode #918

Maximum Sum Circular Subarray this problem is variation of Maximum Sum Subarray question where we implemented the Kadane’s Algorithm. Check out our previous blog post on Kadane’s Algorithm here. Link to the current question https://leetcode.com/problems/maximum-sum-circular-subarray/

Let us consider an array {2, 1, -5, 4, -3, 1, -3, 4, 1}. So according to the problem the array is considered to circular i.e it is connected at both end or end to start. To every maximizing the sum of subarray problem our real objective is to reject the numbers which decrease the sum (negative numbers) and simultaneously find contiguous elements. So, according to our logic can we say this? We are trying to avoid the contiguous element of minimum sum(as most of negative number will be there). We will be finding it soon if this is true.

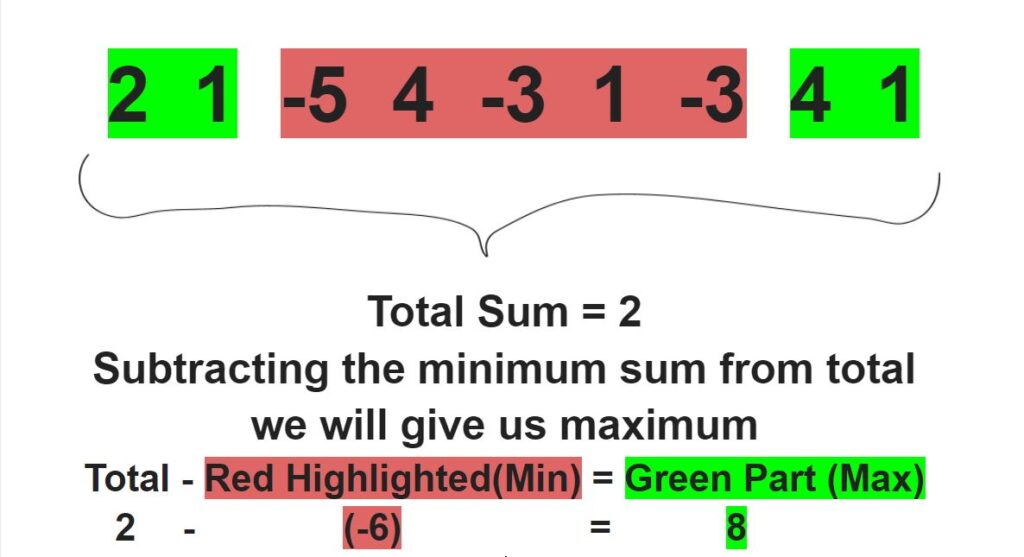
So, by our understanding, we are minimizing the number of bigger negative elements or even all negative elements if beneficial for us. This means we have to reject the subarray with minimum sum. Here we can see the subarray with maximum sum is {4, 1, 2, 1} with sum = 8, which we will be able to get if somehow we can find the minimum sum of subarray. As shown above if subtract the minimum sum from total sum we will get Maximum Sum Circular Subarray.

To find the minimum sum of subarray, why put extra effort building new algorithm? Instead we can invert our array and find the maximum of it. Because now all negative number will be positive and constituting to the max sum. Minimum sum subarray of {2, 1, -5, 4, -3, 1, -3, 4, 1} would be {-5, 4, -3, 1, -3} with sum = -6. So by our approach first we will invert our input array, that will be {-2, -1, 5, -4, 3, -1, 3, -4, -1} and find maximum subarray of this using Kadane’s Algorithm. It will return us {5, -4, 3, -1, 3} with sum = 6. Now we will invert this 6 to -6 because we wanted minimum sum(as all numbers that we are trying to reject were negative). After inverting we will subtract it from total and we will get our Maximum Sum Circular Subarray.

Program to Find Maximum Sum Circular Subarray

Below is the code to function that gives Maximum Sum Circular Subarray :

int maxSubarraySumCircular(int A[]) {
        
        
        int n = A.size();
        int max_straight_SUM = INT_MIN;
        int min_straight_SUM = INT_MAX;
        int array_SUM = 0;
        
        int temp_maxSUM = 0;
        int temp_minSUM = 0;
        
        for(int i=0;i<n;++i)
        {
            array_SUM +=A[i];
            
            temp_maxSUM += A[i];
            max_straight_SUM = max_straight_SUM<temp_maxSUM? temp_maxSUM:max_straight_SUM;
            temp_maxSUM = temp_maxSUM<0?0:temp_maxSUM;
            
            temp_minSUM += A[i];
            min_straight_SUM = min_straight_SUM>temp_minSUM? temp_minSUM:min_straight_SUM;
            temp_minSUM = temp_minSUM>0?0:temp_minSUM;
        }
        if(array_SUM==min_straight_SUM)
            return max_straight_SUM;
        return max(max_straight_SUM,(array_SUM-min_straight_SUM));
    }