LCM of two Numbers in Python

In the previous article we explored about GCD and it’s implementation in Python. Now let us explore the concept of LCM and how we can arrive at the LCM of two Numbers in Python. Before we delve further into Python let us look at a problem which can further/or revise our understanding of LCM. We are given two towers of variant heights:

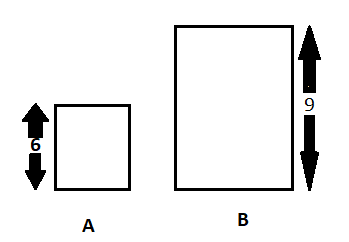
We need to make two blocks using these towers, in tower A we need to use block A and in tower B we need to use block B. We need to make the heights of both towers the same and we need to find the smallest such height which can be made same using only blocks of type A in tower A and only blocks of type B in tower B.

The minimum possible height for reaching parity in height is 18, we can use three blocks of tower A(6*3=18) and three blocks of tower B(9*2=18). 18 is the smallest number which is divisible by 6 and also divisible by 9. In other terms, 18 is the LCM of 6 and 9. The LCM of two numbers where a =4 and b=6 would be 12.

a= int(input("Enter First Number : "))
b =int(input("Enter Second Number : "))
res=max(a,b)
while(res<=a*b):
    if(res%a==0 and res%b==0):
        break;
    res+=1
print("LCM is :", res)

Output:
Enter First Number : 6
Enter Second Number : 9
LCM is : 18

Alternative method obtaining LCM of two numbers in Python

# Python code to demonstrate obtain LCM of two Numbers in Python through the use of the GCD( ) function
# importing "math" library
import math
a=int(input("Enter a : "))
b=int(input("Enter b : "))
gcd=math.gcd(a, b)
lcm=(a*b)/gcd
print("The LCM of the two numbers is : ", lcm)

Output:
Enter a : 6
Enter b : 9
The LCM of the two numbers is :  18.0

Hence, we have explored the concept of LCM and the various ways in which it can be obtained in python for any two given numbers. In the next article we will have a look at Fibonacci Numbers in Python.