Two Pointer Approach: An Efficient Technique

by

In this article we will discuss a linear and constant space technique to solve the programming questions. Two pointer Approach is an efficient technique to solve the problem with optimized time and space complexity. Two Pointer Approach Algorithm is mostly used for solving the array problems, where pointers are actually array indexes.

Whenever the solution depends on the comparison between element pair present in an array in a certain order, this approach should be the first to click in mind. The idea is to reduce the unnecessary comparison of elements by exploiting the implicit order of array element.

There are multiple variations of the Two Pointer Approach, where the two pointers chosen can vary with the initial position or the steps taken at a time. We will focus on the former variant, where we initialize two pointers at both the ends of the array and apply the problem-specific logic updating the pointers until they meet. We will illustrate the approach with a famous 2 Sum Problem.

Problem: Given a sorted array and a target sum, find if a pair exists with the sum equal to the target sum.

Input: arr = {4, 7, 10, 15, 16, 20, 25}, T = 40
Output: True

Naive solution

The simplest approach is to use two for loops nested checking the sum of every possible pair and if it is equal to the given target sum. If a pair exist then return true otherwise false. 

// Naive solution for 2 Sum Problem
bool isSumEqual(int arr[], int n, int T)
{
    for(i = 0 to n-2)
    {
      for(j = i+1 to n-1)
      {
        if(arr[i] + arr[j] == T)
            return true
      }
    }
    return false
}

Time Complexity: O(n2)

Two Pointer Approach

An efficient solution is two use two pointers L and R pointing to the first and the last index of the array. Note that the array is already sorted. Hence, if the sum of element at two indexes L and R is larger than the sum, this means that incrementing the L pointer will further increase the sum. So in this case we decrement the R pointer. So we compute the sum of elements at L and R if the sum is equal to the target return true. Else if the sum is less than the target we increment the L pointer, and if greater than the target, decrement the R pointer. The loop stops if either we get the required pair or if the L pointer and R pointer meets. When L and R become equal, none of the pair sums was equal to the target, hence return false.

Two Pointer Approach
Two Pointer Approach for 2 Sum Problem
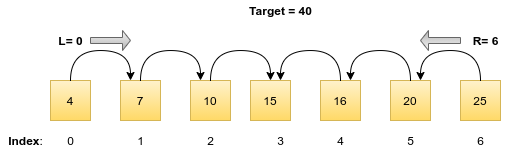
// Two Pointer approach for finding is a pair exist with sum equal to a given target in a sorted array
bool isSumEqual(int arr[], int n, int T)
{
    L = 0
    R = n-1 
    while( L < R)
    {
        tempsum = arr[i] + arr[j]
        if ( tempsum == T)
            return true
        else if ( tempsum < T )
            L = L + 1
        else if ( tempsum > T )
            R = R - 1
    }
    return false
}

Time Complexity: O(n). Only one traversal of the array is needed from both ends of the array.
Auxiliary space: O(1). As only constant space is used.

There are many applications of the two pointer approach:

Read similar articles here: Find square root of an integer

Leave a Comment