Merge Sort Algorithm: An Efficient Sorting Approach

In this article, we will learn about Merge Sort Algorithm. There are many well known sorting algorithms but the cool thing about Merge sort is that it takes O(log n) time complexity even in the worst case. Merge sort is a sorting algorithm based on the Divide and Conquer technique. The approach is to transform the problem into multiple subproblems and solve each subproblem individually and combine the results to get back the solution to the original subproblem.

The Merge sort works in two-phase:
Divide: Divide the array into two equal halves until we get each subarray of size one.
Merge: Merge the two equal halves recursively producing a new sorted array. This procedure is repeated recursively until we get the final array.

Working of Merge Sort Algorithm

Let us understand with an example: Arr= {5,24, 8, 1, 3, 16, 10 , 20}
In the divide phase, We initialize the two pointers tracking the first and last index as l and r respectively, and the mid index as m.
Then partition the array as A[l..m] and A[m+1, r]. Now we get the two sub-arrays. We repeat this process by dividing the array into two equal halves from the mid index m until we have all the subarray of length 1 and no more divide is possible. This can be done recursively as we see in the implementation below.

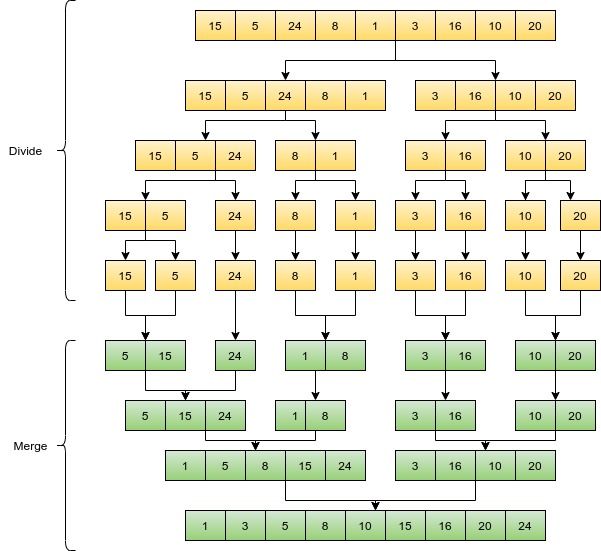
In the Merge phase, we are merging the two halves while sorting the individual elements from each half.  Initialize a new array Arr of the length of the sum of left and right half. Initialize two  Index p1 and p2 pointing to the first element of both subarray respectively , then if the left[p1]<right[p2], then add the smaller element i.e. left[p1] to the Arr, and update the index p1 to p1+1 and then check if  left[p1]<right[p2].

This comparison and updating the new array with the smaller of the two elements is followed until we reach the end of one of the subarray. Then we append the remaining elements of the other subarray to the merged array Arr. In this manner, every two halves are merged, and we get the original array, sorted.

C++ Implementation of Merge Sort Algorithm

//Merge the two sorted  array to a single sorted array
void merge(int arr[], int l , int m , int r)
{
    int i, j, k;
    int n1= m-l+1;
    int n2= r-m;
    int L[n1], R[n2];
    
    for(int i = 0;i<n1;i++)
        L[i]=arr[l+r];
    for(int j= 0; j<n2;j++)
        R[i]= arr[m+1+j];
    i=0;
    j=0;
    k=0;
    while((i<n1)&&(j<n2))
    {
        if(L[i]<= R[i])
        {
            arr[k]=L[i];
            i++;
        }
        else
        {
            arr[k]= R[j];
            j++;
        }
        k++;
    } 
    while(i<n1)
    {
        arr[k] = L[i];
        i++;
        k++;
    }
     while(j<n2)
    {
        arr[k] = R[i];
        j++;
        k++;
    }
}
}
//Recursive call to mergeSort for each half of the array
void mergeSort(int arr[], int l , int r)
{
    if(l< r)
    {
        int m - l+(r-1)/2;
        mergeSort(arr, l, m)
        mergeSort(arr, m+1, r)
        merge(arr, l, m ,r )
    }
}

Time Complexity: Merge sort is an efficient algorithm that gives better time complexity in the worst case as compared to other sorting algorithms such as Selection sort, Insertion sort, Quicksort. The worst-case performance of Merge sort is O(n log n). The time complexity can be analyzed from the recurrence relation T(n) = 2T(n/2) + n . 
Best case: O(n log n )
Average case: O(n log n )
Worst case: O(n log n )

Auxilliary space: O(n)

Check out other articles here: Median of two sorted Arrays, Find Repeating element in array.